Step7
この例では相対的に高いレベルの測定の為、センサのノイズによる要素の計算は通常無視してもよいと考えますが、今回の例では念の為計算をします。初期値のフィルタリング機能と変調モードを用いたと仮定します。
また、信号レベルは13dBm(20mW)です。57518センサのRMSノイズとドリフトはマニュアルから50nWです。ノイズの標準不確かさはこれら2つの値の比です。

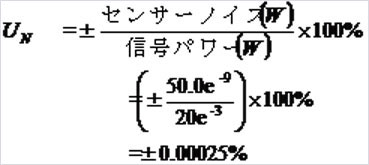
Step8
センサのゼロドリフトの標準不確かさは、Step7で算出された結果に含まれるため、この項目はスキップします。

Step9
センサ校正係数(CalFactor)の標準不確かさは、マニュアルに記載されている不確かさの値から補正する必要があります。
1GHzにおいてセンサ校正係数の標準不確かさは1.7%であり、また0.5GHzにおいては1.6%です。ここでのポイントは、測定周波数に非常に近い1GHzの周波数で校正を行なっている事です。これは、1GHzにおいてセンサ校正係数による要素がゼロになるという事を意味します。
概算値として0.5GHzと1GHzの間の線形性補正を使用します。900MHzは1GHzから500MHzに20%（5分の1）低い値です。従って、計算式は以下のようになります。

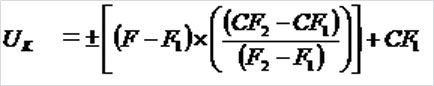
ここで【F=0.9、F1=0.5、F2=1.0、CF1=1.6、CF2=0.0】ですので、

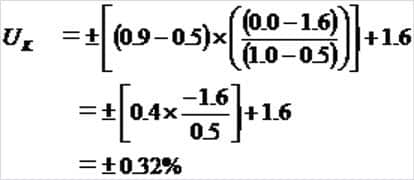
Step10
今、個々の標準不確かさの要素が算出されたため、これら値を用いて不確かさの“バジェットシート”を作成し、合成標準不確かさUcと拡張不確かさUを求めます。

この例からわかる事は、測定が校正周波数に近い場合は整合がかなりよい為、不確かさを大きくしている要因は、線形性による標準不確かさとレベルの標準不確かさによるものです。尚、拡張不確かさ5.17%は読み値の約0.22dBの不確かさに該当します。

最後に

今回は、計算ばかりで少し複雑になりましたが、測定の性能を理解する場合は、単純に機器本体やセンサの精度で評価できるものでは無くまた、単純な足し算ではダメである事がわかって頂けたかと思います。

もし、高性能な測定機器を用いて測定したにも関わらず、満足いく結果が得られない場合は、一度これらに関して確認して頂ければと思います。